引言
根據液滴表面張力分析的結果,近軸情況下所有的液滴都可以當成半球來處理,這裡分析液滴的放大倍率。
模型
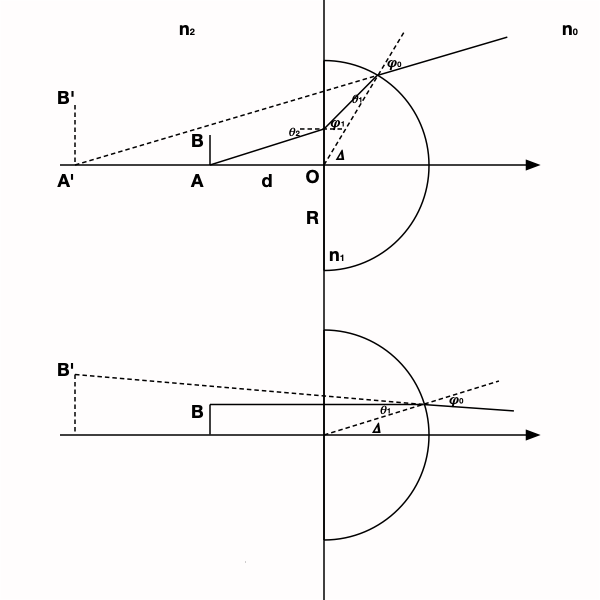
光路如圖所示,透過半徑為$R$的半球觀察屏幕下方$d$處的一個物體$AB$,其成像在$A’B’$。上下兩張示意圖分別為$A$和$B$發出的光線。屏幕,半球,空氣的折射率分別為$n_2$,$n_1$,$n_0$。
計算
先考慮從$A$發出的光線,根據折射定律有
$$
n_2\sin\theta_2^A = n_1\sin\varphi_1^A
$$
上標表示從$A$發出的光,後面對$B$同理。從球面射出光線的與法線的夾角為$\theta_1^A$,根據正弦定理有
$$
\frac{\sin\theta_1^A}{\tan\theta_2^Ad} = \frac{\sin\left(\varphi_1^A + \frac{\pi}{2}\right)}{R}
$$
然後根據折射有
$$
n_1\sin\theta_1^A = n_0\sin\varphi_0^A
$$
這樣每個量都可以根據入射角$\theta_2^A$解出來。由幾何關係可以得到
$$
\left( \lvert A’A \rvert + d + R\cos\Delta^A \right)\tan\left(\Delta^A-\varphi_0^A\right) = R\sin\Delta^A
$$
其中$\Delta^A = \varphi_1^A + \theta_1^A$。注意這裡面所有的入射角和折射角都很小,最後可以解得像的位置
$$
\lvert AA’ \rvert \approx \left[ \frac{\frac{n_2}{n_1}+\frac{d}{R}}{\frac{n_2}{n_1}+\frac{d}{R}-\frac{n_1d}{n_0R}} - 1\right]R - d = \frac{n_1^2d}{n_0n_2R + n_0n_1d - n_1^2d}\cdot R - d
$$
接下來考慮從$B$發出的光線,根據折射定律有
$$
n_1\sin\theta_1^B = n_0\sin\varphi_0^B
$$
根據幾何關係
$$
\lvert A’B’ \rvert = \lvert AB \rvert + \tan\left(\varphi_0^B - \Delta^B\right)\left(\lvert AA’ \rvert + d + R\cos\Delta^B\right)
$$
其中$\Delta^B = \theta_1^B$,並注意$\lvert AB \rvert = R\sin\Delta^B$ ,最後解得
$$
\beta \equiv \frac{\lvert A’B’ \rvert}{\lvert AB \rvert} \approx 1 + \left(\frac{n_1}{n_0}-1\right)\left(\frac{n_1^2d}{n_0n_2R + n_0n_1d - n_1^2d} + 1\right)
$$
分析
下面做一點簡單的分析。
取空氣和水的折射率分別為$n_0 = 1$,$n_1 = 4/3$,結果可以簡化為
$$
\beta \approx \frac{12n_2\eta}{9n_2\eta -4}
$$
其中$\eta = R / d$。當液滴很大時$\eta \to \infty$,$\beta \approx 4/3$將等於一個定值。反之當$\eta \to [4/(9n_2)]^+$時則有無限大的放大倍率,這是因為此時從$A$發出的光線將平行於主光軸。
考慮$\varphi_0^A > \Delta^A$的一般情況,解得
$$
\eta < \frac{n_1}{n_2}\left( \frac{n_1}{n_0} - 1 \right)
$$
定義臨界比值
$$
\eta_c = \frac{n_1}{n_2}\left( \frac{n_1}{n_0} - 1 \right)
$$
小於這個值,像將成在液滴上方,即示意圖中半球右側,是個倒立的實像。當$\eta \to \eta^-$將成像在右側無窮遠處,人是看不到這個像的。因此減小$R$將導致一個不連續的變化,可以用這一性質測量屏幕的折射率$n_2$。