引言
這裡考慮潮汐的形狀。
模型
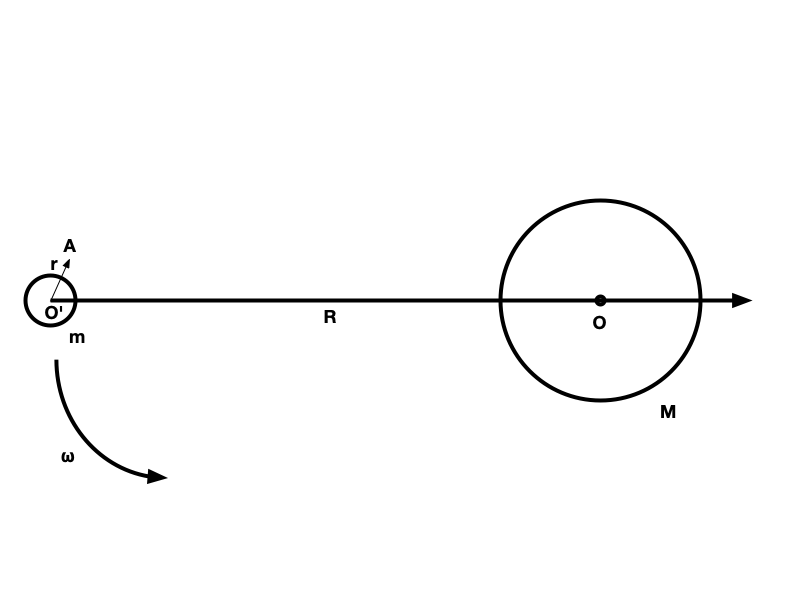
考慮質心$O’$,質量為$m$的球繞質量為$M$,質心為$O$的球以角速度$\omega$逆時針旋轉。現在考慮$O’$附近任意點$A$,質量為$m_0$,用$\theta$表示$\vec{O’A}$和$\vec{O’O}$的夾角。記$\vec r = \vec{O’A}$,$\vec R = \vec{OO’}$,以及$\vec R_A = \vec R + \vec r$。
現在以$O’$為參考系,即考慮$O$圍繞其旋轉。由於$O’$是非慣性系,需要引入慣性離心力。考察$O’$點的受力
$$
\vec F_{O’}^t = -\frac{GMm}{R^3}\vec R - m\vec \omega \times(\vec \omega \times \vec R) = -\frac{GMm}{R^3}\vec R + m\omega^2\vec R = \vec 0
$$
上標$t$表示潮汐力。第一項表示$O$在該點的引力,後一項為慣性力,兩個力平衡使得$O’$處於靜止狀態。由以上結果可以得到$GM = \omega^2R^3$。
和上面類似,現在考慮$A$處潮汐力。由於$O’$是平動,$A$與$O’$有共同的離心加速度
$$
\vec F_A^t = -\frac{GMm_0}{R_A^3}\vec R_A + m_0\omega^2\vec R
$$
考慮近似$r \ll R$
$$
\frac{\vec R_A}{R_A^3} = \frac{\vec R + \vec r}{R_A}\frac{1}{R^2}\frac{1}{1 + \frac{r^2}{R^2} - 2\cos\theta\frac{r}{R}} \approx \frac{1}{R^3}\left(\vec R + \vec r + 2r\cos\theta\frac{\vec R}{R}\right)
$$
代入整理得到
$$
\vec F_A^t \approx -m_0\omega^2\left(\vec r + 2r\cos\theta\frac{\vec R}{R}\right)
$$
勢能
考慮$\vec r$方向單位矢量為$\hat r$,$\theta$增大方向的單位矢量為$\hat \theta$。將單位矢量$\vec R/R$表示為
$$
-\frac{\vec R}{R} = \cos\theta\hat r - \sin\theta\hat\theta
$$
代入潮汐力
$$
\vec F_A^t \approx -m_0\omega^2\left(r\hat r - 2r\cos^2\theta\hat r + r\sin2\theta\hat\theta\right)
$$
引入勢函數$\phi_1(r,\theta)$,考慮$-\nabla \phi_1(r,\theta) = \vec F_A^t / m_0$,勢函數可以寫成
$$
\phi_1(r,\theta) = C_1r^2\left( \frac{1}{2} - \cos^2\theta \right)
$$
其中$C_1 = \omega^2$。現在考慮$O’$自身的引力,這裡需要做一個假設,考慮潮汐只影響表層的海水,勢函數寫成
$$
\phi_2(r,\theta) = -\frac{Gm}{r} = -\frac{C_2}{r}
$$
其中$C_2 = m\omega^2R^3/M$。對表層海水而言,勢函數是兩者之和,可以差一個不影響結果的常數,這裡令其為零
$$
\phi(r,\theta) = \phi_1(r,\theta) + \phi_2(r,\theta) = C_1r^2\left( \frac{1}{2} - \cos^2\theta \right) - \frac{C_2}{r}
$$
現在考慮邊界$r = r_1(\theta)$是角度的函數,考慮$r > r_0$表層海水總勢能
$$
\begin{equation}
\begin{aligned}
\Phi(r_1) =& \int_{-\pi}^\pi d\varphi \int_{-\pi}^\pi d\theta \int_{r_0}^{r_1}dr \rho r^2\sin\theta \phi(r,\theta)\\
=& 2\pi\rho \int_{-\pi}^\pi d\theta \left[ \frac{C_1}{5}\left( \frac{1}{2} - \cos^2\theta \right)\sin\theta r_1^5 - \frac{C_2}{2}\sin\theta r_1^2 \right] + const
\end{aligned}
\end{equation}
$$
$\rho$是海水密度。考慮約束條件液體的體積是一定的
$$
\int_{-\pi}^\pi d\varphi \int_{-\pi}^\pi d\theta \int_{r_0}^{r_1}dr \rho r^2\sin\theta = 2\pi\rho \int_{-\pi}^\pi d\theta \frac{r_1^3}{3}\sin\theta = const
$$
考慮拉氏乘子並改寫泛函
$$
\tilde\Phi(r_1) = 2\pi\rho \int_{-\pi}^\pi d\theta \left[ \frac{C_1}{5}\left( \frac{1}{2} - \cos^2\theta \right)\sin\theta r_1^5 - \frac{C_2}{2}\sin\theta r_1^2 + \lambda\frac{r_1^3}{3}\sin\theta \right] + const
$$
令$\delta\tilde\Phi(r_1) = 0$,得到
$$
C_1\left( \frac{1}{2} - \cos^2\theta \right)\sin\theta r_1^4 - C_2\sin\theta r_1 + \lambda\sin\theta r_1^2 = 0
$$
考慮$r_1 \neq 0$以及$\theta \neq 0, \pi$,得到
$$
-\frac{1}{2}C_1\cos2\theta r_1^3 - C_2 + \lambda r_1 = 0
$$
考慮近似$r_1 = r_0 + \delta r$,其中$\delta r \ll r_0$,代入得
$$
\delta r \approx \frac{\frac{1}{2}C_1\cos2\theta r_0^3 + C_2 - \lambda r_0}{\lambda - \frac{3}{2}C_1\cos2\theta r_0^2}
$$
最後得到
$$
r_1 \approx r_0 + \frac{\frac{1}{2}C_1\cos2\theta r_0^3 + C_2 - \lambda r_0}{\lambda - \frac{3}{2}C_1\cos2\theta r_0^2} = \frac{-C_1\cos2\theta r_0^3 + C_2}{\lambda - \frac{3}{2}C_1\cos2\theta r_0^2}
$$
將液體的總質量記為$m_1$,解出$r_1$代回約束條件即可解出乘子
$$
\begin{equation}
\begin{aligned}
m_1 \approx& 2\pi\rho \int_{-\pi}^\pi d\theta r_0^2\delta r\sin\theta\\
=& -2\pi\rho r_0^2 \int_{-\pi}^\pi \frac{\frac{1}{2}C_1\cos2\theta r_0^3 + C_2 - \lambda r_0}{\lambda - \frac{3}{2}C_1\cos2\theta r_0^2} d\cos\theta\\
=& -2\pi\rho r_0^2 \int_{-1}^{1} \frac{\frac{1}{2}C_1 (2x^2-1) r_0^3 + C_2 - \lambda r_0}{\lambda - \frac{3}{2}C_1 (2x^2-1) r_0^2} dx\\
=& -2\pi\rho r_0^2 \int_{-1}^{1} \frac{Dx^2 + E}{-Fx^2 + G}dx\\
=& -2\pi\rho r_0^2 \left[ -\frac{2D}{F} + \frac{2(EF+DG)}{\sqrt{F^3G}} \tanh^{-1}\left(\sqrt{\frac{F}{G}}\right) \right]\\
\approx& -2\pi\rho r_0^2 \left[ -\frac{2D}{F} + \frac{2(EF+DG)}{\sqrt{F^3G}} \sqrt{\frac{F}{G}} \right]\\
=& 4\pi\rho r_0^2\frac{\frac{1}{2}C_1r_0^3 - C_2 + \lambda r_0}{\lambda + \frac{3}{2}C_1r_0^2}
\end{aligned}
\end{equation}
$$
其中$D = C_1r_0^3$,$E = -\frac{1}{2}C_1r_0^3 + C_2 - \lambda r_0$,$F = 3C_1r_0^2$,$G = \lambda + \frac{3}{2}C_1r_0^2$。中間假設了$F/G \to 0$,解出的$\lambda$滿足這個條件。代回$r_1$即可以得到
$$
r_1 = \frac{(r_0-C_3)\left[ -C_1\cos2\theta r_0^3 + C_2 \right]}{\frac{1}{2}C_1r_0^3\left[ -(1 + 3\cos2\theta) + 3\frac{C_3}{r_0}(1 + \cos2\theta) \right] + C_2}
$$
其中$C_3 = m_1/(4\pi\rho r_0^2)$表示水層平均高度。
分析
現在對結果作一點分析。
考慮近似,$r_0 \gg C_3$,則
$$
r_1 \approx \frac{r_0\left[ -C_1\cos2\theta r_0^3 + C_2 \right]}{-\frac{1}{2}C_1r_0^3 (1 + 3\cos2\theta) + C_2}
$$
$r_1$的分佈與角度有關,儘管在分析中略去了$\theta = 0,\pi$的位置,考慮函數的連續性,考慮
$$
\lim_{\theta \to 0} r_1(\theta) = \frac{r_0\left[ -C_1r_0^3 + C_2 \right]}{-2C_1r_0^3 + C_2}
$$
對應高潮。現在考慮兩側
$$
r_1\left(\theta = \frac{\pi}{2}\right) = \frac{r_0C_2}{C_1r_0^3 + C_2}
$$
對應低潮。高低潮的差為
$$
\Delta = \left[ \lim_{\theta \to 0} r_1(\theta) \right] - r_1\left(\theta = \frac{\pi}{2}\right) = \frac{C_1r_0^4(-C_1r_0^3 + 2C_2)}{(-2C_1r_0^3 + C_2)(C_1r_0^3 + C_2)}
$$
令$\eta = C_1r_0^3/C_2 = Mr_0^3/(mR^3)$,這個比值是一個遠小於一的正數
$$
\Delta = r_0\frac{\eta(2-\eta)}{(1-2\eta)(1+\eta)}
$$
若$R$非常大,潮差可以近似為
$$
\Delta \approx 2\eta r_0 = 2\left(\frac{M}{m}\right)\left(\frac{r_0}{R}\right)^3\cdot r_0
$$
$r_1$也可以近似為
$$
\frac{r_1}{r_0} = \frac{1 - \cos2\theta\eta}{-\frac{1}{2}\eta (1 + 3\cos2\theta) + 1} \approx 1 + \eta\cos^2\theta
$$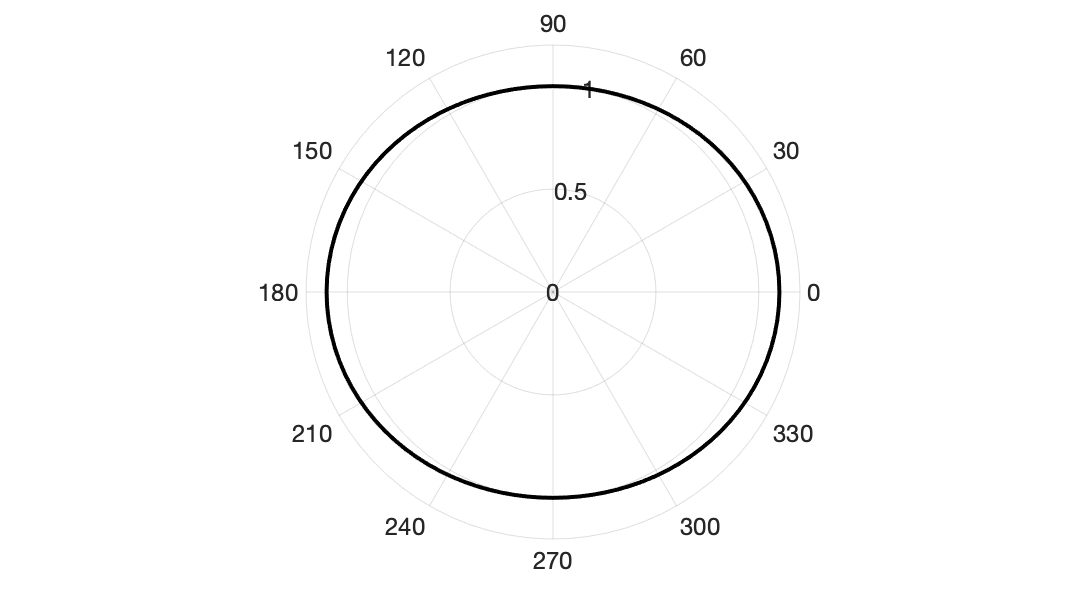
$r_1/r_0$的結果如上圖所示,為了展示細微的差別,這裡取了較大的$\eta = 0.1$。
順便估計地球上的潮差,地球質量相當於$81.3$倍月球質量,地月距離相當于$60$個地球半徑,以地球半徑近似估算$r_0$,代入數據可以算出$\Delta_M \approx 0.73\text{m}$。以及太陽質量大約是地球的$3.3 \times 10^5$倍,日地距離相當于地球半徑的$2.3 \times 10^4$倍,代入數據可以算出$\Delta_S \approx 0.35\text{m}$。這和開放海洋中潮差在$0.6-1\text{m}$範圍的數據在同一個量級。
注意的是潮汐受很多因素影響,這裡僅僅是最低階的估計。