引言
如果將數獨寫成矩陣形式,並考慮有限次的行列交換將求解過程轉化爲一系列代數方程:這種方法只有在選擇適當的初始矩陣有效,因為不同種的初始矩陣無法通過直接的行列交換來實現轉化,換言之這些矩陣的行列式的絕對值通常不相等。
即便這樣初始矩陣可以找到,而且這樣的初始矩陣已經滿足一些性質(比如每個數字在一行或者一列都出現一次,交換不改變這個性質),但宮間不能出現重複數字依然是一個需要在求解後附加上的限制。因為需要面對大量的不同種類的初始矩陣,這種方法並不簡便,也不可行。
這裡考慮一個直接的辦法。
模型
我們考慮不同命題$p^1$和$p^2$的關係,不難發現只有如下幾中可能
- $p^1 \rightarrow p^2$,表示由前者可以得到後者
- $\neg p^1 \rightarrow \neg p^2$,即$p^2 \rightarrow p^1$,表示由後者可以得到前者
- $\neg p^1 \rightarrow p^2$,表示兩者不能同時不成立
- $p^1 \rightarrow \neg p^2$,表示兩者不能同時成立
- $p^1 \leftrightarrow p^2$,表示兩者相同
- $p^1 \leftrightarrow \neg p^2$,表示兩者相反
考慮如下兩種情況,存在命題$p^1$,$p^2$和$p^3$:
- 若$\neg p^1 \rightarrow p^2 \rightarrow \neg p^3 \rightarrow p^1$,即$\neg p^1 \rightarrow p^1$,可得$p^1 = \top$
- 若$p^1 \rightarrow \neg p^2 \rightarrow p^3 \rightarrow \neg p^1$,即$p^1 \rightarrow \neg p^1$,可得$p^1 = \bot$
如果用$+$和$-$表示命題和其否定,則以上關係可以用無向圖表示為
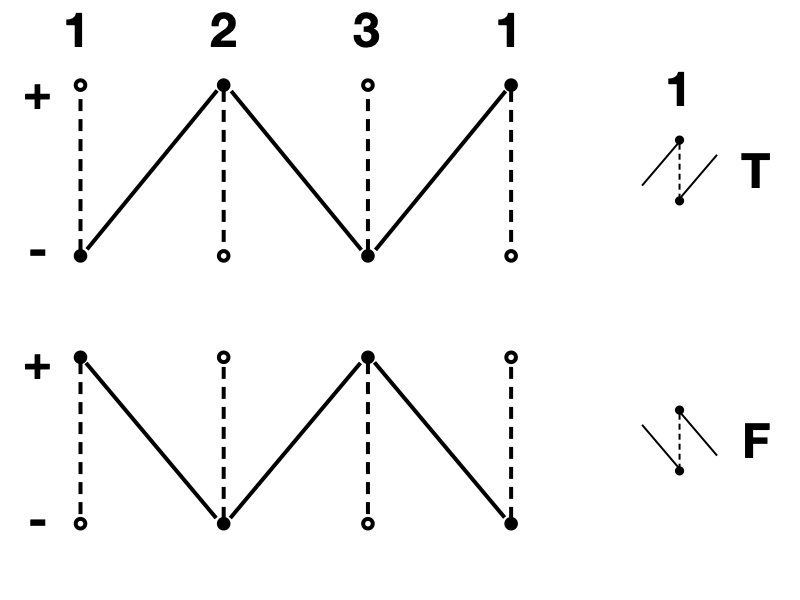
現在考慮數獨的情況,規定記號$p_{ij}^m$於數獨第$i$行,第$j$列填入數字$m$。同樣可以用$p_{ij}^{m+}$和$p_{ij}^{m-}$在圖中表示$p_{ij}^m$和$\neg p_{ij}^m$,它們將構成一張圖的全部頂點,數獨的求解等價於尋找連接$p_{ij}^{m+}$和$p_{ij}^{m-}$的過程。
對於數獨每格只能填入一個數字,以及每行,每列,每宮(Block)同一數字不能超過兩次,有以下性質
$$
\begin{align}
& p_{ij}^m \rightarrow \neg p_{ij}^n, \qquad m \neq n,\\
& p_{ij}^m \rightarrow \neg p_{ik}^m, \qquad j \neq k,\\
& p_{ij}^m \rightarrow \neg p_{kj}^m, \qquad i \neq k,\\
& p_{ij}^m \rightarrow \neg p_{kl}^m, \qquad (i,j),(k,l) \in B,\quad i \neq k,\quad j \neq l,
\end{align}
$$
這些都是要求命題不能同時成立,即圖中向下的直線,如果考慮從一個命題的兩個端點出發,僅有這些條件無法形成環。
如果要形成環,則需要考慮以下情況:一個格子中只剩兩個候選數$m$和$n$,以及候選數$m$只能出現在每行,每列,每宮的兩個位置
$$
\begin{align}
& \neg p_{ij}^m \rightarrow p_{ij}^n, \qquad m \neq n,\\
& \neg p_{ij}^m \rightarrow p_{ik}^m, \qquad j \neq k,\\
& \neg p_{ij}^m \rightarrow p_{kj}^m, \qquad i \neq k,\\
& \neg p_{ij}^m \rightarrow p_{kl}^m, \qquad (i,j),(k,l) \in B,\quad i \neq k,\quad j \neq l,
\end{align}
$$
這些都是要求命題不能同時不成立,即圖中向上的直線,結合向下的直線則可能成環,而後則可以根據圖中情況來確認,或者刪去格中候選數。一旦格中候選數得到確認,或者僅剩一個候選數(包括格中某個候選數在其所在行,列,宮唯一的情況,則可以直接確認該格),按其所在行,列,宮排除其他候選並更新無向圖即可。
考慮無向圖的鄰接矩陣$\mathbf{A}$,數獨求解等價於尋找$p_{ij}^{m-} \to p_{ij}^{m+}$或$p_{ij}^{m+} \to p_{ij}^{m-}$的路徑,假設其分別對應為$A_{rs} = 0$和$A_{sr} = 0$。現在依次增加矩陣的階$\mathbf{A^k}$,其中$k = 2,3,…$,若存在$(A^k)_{rs} \neq 0$或$(A^k)_{sr} \neq 0$,則可以分別判斷出命題$p_{ij}^m$的真或假。由於鄰接矩陣可能是一個巨大的稀疏矩陣,亦可用遞歸的方式搜索節點。
後記
這是對此前一篇文章的補充,當時我並不知道邏輯運算。
上個月我在醫院候診的椅子上等待治療牙齒,我凝視著地上的格子,萌生了交換循環矩陣行列的想法。
我認為這是一個聰明的點子,由此我可以把求解過程轉化為代數方程。但只可惜,它不管用,因為我很快就發現不能通過行列交換而實現轉化的數獨矩陣。在經過一些失敗的嘗試後我又回到多年以前的想法:我在整理以前的結果時發現求解過程僅僅對應路徑的尋找,僅僅從幾個簡單的約束條件出發,而不需要考慮一切冗余的技巧。