引言
這篇將證明Wigner Semicircle Law,它講述一個隨機矩陣的特徵值將分佈在一個半圓上。
證明
考慮一個隨機$N \times N$矩陣$\mathbf J$,它的每個非對角元素都服從均值為零,方差為$1/N$的高斯分佈,而對角元素方差為$2/N$。這裡介紹格林函數$G(z)$,它指的是
$$
\int d\lambda’\frac{\rho(\lambda’)}{z-\lambda’} = \frac{1}{N}\sum_{i=1}^{N}\frac{1}{z-\lambda_i} = G(z)
$$
其中$G(z) = \frac{1}{N}\text{Tr}(z\mathbf{I}-\mathbf{J})^{-1}$,密度定義為
$$
\rho(\lambda’) = \frac{1}{N}\sum_{i=1}^N\delta(\lambda’-\lambda_i)
$$
此外還需要Plemelj Formula,指的是
$$
\rho(\lambda) = \frac{1}{\pi}\lim_{\epsilon \to 0^+}\text{Im}G(\lambda-i\epsilon)
$$
它可以被簡單證明,不在這裡展開,因為不需要求出柯西主值,這是此處取虛部的原因。考慮
$$
G(z) = \frac{1}{N}\sum_{i=1}^{N}\frac{1}{z-\lambda_i} = \frac{1}{N}\partial_z\ln\prod_{i=1}^N(z-\lambda_i) = \frac{1}{N}\partial_z\ln\det(z\mathbf I - \mathbf J)
$$
這是因為對多維高斯積分有結論
$$
\int d^Nx\exp[-\frac{1}{2}\sum_{ij}x_iA_{ij}x_j] = (2\pi)^{N/2}/\sqrt{\det(\mathbf A)}
$$
這樣就可以把行列式換掉,即可得到
$$
G(z) = -\frac{2}{N}\partial_z\ln\det(z\mathbf I - \mathbf J)^{-1/2} = -\frac{2}{N}\partial_z\ln Z
$$
其中
$$
Z = \int\mathcal Dx \exp[-\frac{1}{2}\sum_{ij}x_i(z\mathbf I - \mathbf J)_{ij}x_j]
$$
注意$\mathcal Dx = \prod dx/(2\pi)^{N/2}$。現在需要對其配分函數做平均(這一步是有問題的,見後記)
$$
\begin{equation}
\begin{aligned}
\langle Z \rangle =& \int\prod_i \frac{dx_i}{(2\pi)^{N/2}}\exp[-\frac{z}{2}\sum_ix_i^2]\int\prod_{ij}dJ_{ij}P(J_{ij})\prod_i\exp[\frac{1}{2}J_{ii}x_i^2]\prod_{i<j}\exp[x_iJ_{ij}x_j]\\
=& \int\prod_i \frac{dx_i}{(2\pi)^{N/2}}\exp[-\frac{z}{2}\sum_ix_i^2 + \frac{1}{4N}\sum_{ij}(x_ix_j)^2]
\end{aligned}
\end{equation}
$$
現在,需要引入一個序參量
$$
q = \frac{1}{N}\sum_i x_i^2
$$
以及相應的限制
$$
\begin{equation}
\begin{aligned}
\langle Z \rangle =& \int\prod_i\frac{dx_i}{(2\pi)^{N/2}} \int dq \delta\left(q-\frac{1}{N}\sum_i x_i^2\right)\exp[-\frac{zN}{2}q + \frac{N}{4}q^2]\\
=& \int\frac{dq}{(2\pi)^{N/2}}\frac{dk}{2\pi}\left[\int\prod_idx_i\exp[-\frac{ik}{N}\sum_ix_i^2]\right]\exp[ikq-\frac{zN}{2}q+\frac{N}{4}q^2]
\end{aligned}
\end{equation}
$$
做一次換元$\eta = 2k/N$然後估計這個積分
$$
\begin{equation}
\begin{aligned}
\langle Z \rangle =& \frac{N}{4\pi}\int\frac{dq}{(2\pi)^{N/2}}\int d\eta \left[\int\prod_idx_i\exp[-\frac{i\eta}{2}\sum_ix_i^2]\right]\exp[\frac{iN\eta q}{2}-\frac{zN}{2}q+\frac{N}{4}q^2] \\
=& \frac{N}{4\pi}\int dq\int d\eta \exp[\frac{N}{2}\mathcal L]
\end{aligned}
\end{equation}
$$
其中$\mathcal L = i\eta q - \ln(i\eta) - zq + q^2/2$。考慮拉普拉斯近似來處理這個積分,物理上也叫Saddle-Point Method。分別取微分得到
$$
\frac{\partial\mathcal L}{\partial\eta} = iq - 1/\eta = 0
$$
以及
$$
\frac{\partial\mathcal L}{\partial q} = i\eta - z + q = 0
$$
解出$q_0 = \frac{z \pm \sqrt{z^2-4}}{2}$,以及$\eta_0 = 1/(iq_0)$。最後結果要取對數,直接保留指數項而略去前面所有的係數
$$
\langle Z \rangle \approx \exp[\frac{N}{2}\mathcal L_0] = \exp{\frac{N}{2}[1+\ln q_0-zq_0+q_0^2/2]}
$$
因此
$$
G(z) = -\frac{2}{N}\partial_z\ln\langle Z\rangle = -\left(\frac{1}{q_0}-z+q_0\right)\frac{\partial q_0}{\partial z} + q_0 = q_0
$$
現在考慮$\epsilon \to 0^+$,得到
$$
\rho(\lambda) = \frac{1}{\pi}\lim_{\epsilon \to 0^+}\text{Im}G(\lambda-i\epsilon) = \frac{1}{2\pi}\lim_{\epsilon \to 0^+}\text{Im}\left[\lambda-i\epsilon \pm \sqrt{(\lambda-i\epsilon)^2-4}\right] = \frac{\sqrt{4-\lambda^2}}{2\pi}
$$
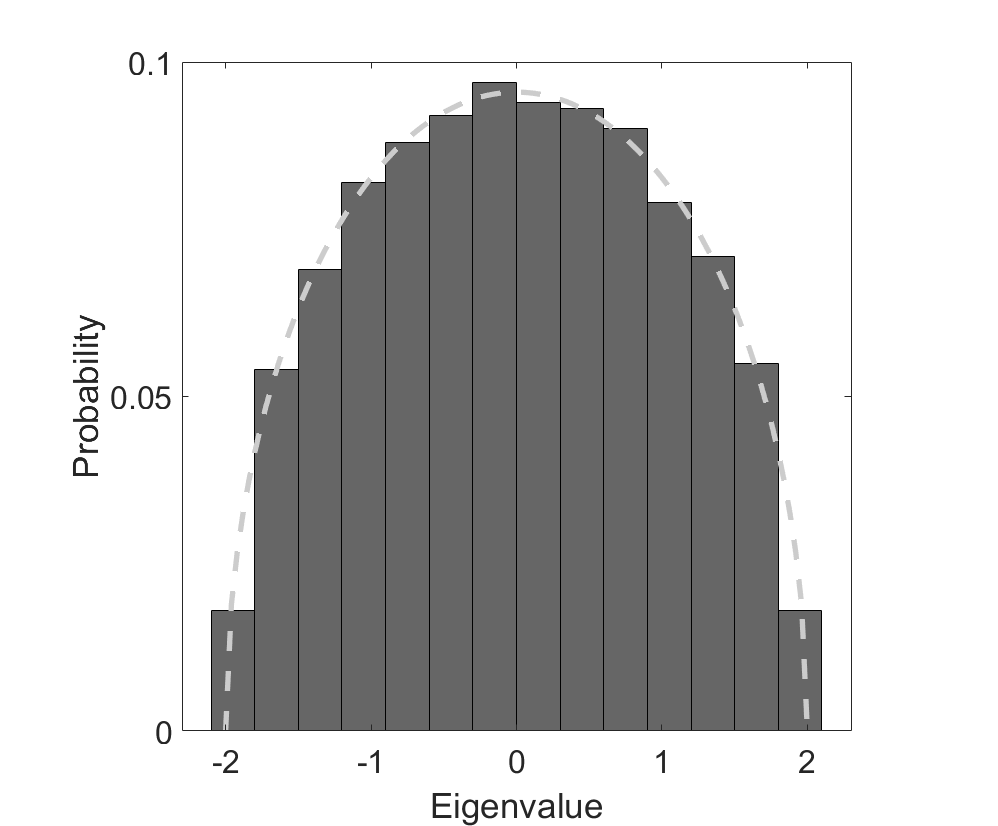
這就是半圓定理。
後記
注意$\langle Z\rangle$和$\langle \ln Z\rangle$是不同的,前者對於退火而後者對於淬火,但在此處給出一樣的結果。
格林函數的嚴格寫法應該是
$$
G(z) = \frac{1}{N}\langle \sum_{i=1}^{N}\frac{1}{z-\lambda_i}\rangle = \frac{1}{N}\langle\text{Tr}(z\mathbf{I}-\mathbf{J})^{-1}\rangle
$$