引言
月底要回香港,我可能沒有時間打理Blog。時間是虛標的,真實時間為一個禮拜前(2022/02/22)。具體的發布時間沒有意義,因為文章是很早就已經寫好的。
我對木星內部的金屬氫很感興趣,計算液體金屬氫的具體位置則需要知道內部的壓強分佈。
模型
暫時考慮單一氣體的巨行星,假設密度正比於壓力
$$
\rho = c_0p
$$
係數$c_0$可以通過狀態方程解出。
方程
對一小塊立體角$d\Omega$所對應的球面分析,取向外為正方向,用$r$表示距離球心的距離
$$
\left[p(r = r) - p(r = r + dr)\right]drd\Omega -\frac{G}{r^2}\left[\int_0^r \rho 4\pi r^2dr\right]\left[\rho r^2drd\Omega\right] = 0
$$
帶入密度並取一次微分,得到
$$
rp’’p - rp’^2 + 2pp’ + 4\pi Gc_0^2rp^3 = 0
$$
或者寫成
$$
\frac{d}{dr}\left[r^2\frac{p’}{p}\right] + 4\pi Gc_0^2r^2p = 0
$$
令$p = k\tilde p$,其中$k = 1/(4\pi Gc_0^2)$,方程簡化為
$$
\frac{d}{dr}\left[r^2\frac{\tilde p’}{\tilde p}\right] + r^2\tilde p = 0
$$
令$q = \ln\tilde p$,則方程可以簡化為
$$
q’’ + \frac{2}{r}q’ + e^q = 0
$$
這個方程可能無法直接解出,下面考慮其漸近行為。
漸近行為
考慮半徑很大時,方程可以近似為
$$
q’’ + e^q \approx 0
$$
這是因為壓強變化在遠處有界。以及在半徑很小時,方程近似處理為
$$
q’ \approx 0
$$
表示中心處壓強是一個定值,與經驗一致。下面我們解第一個方程,考慮
$$
q’q’’ + q’e^q = 0
$$
兩邊同時乘上導數,這是因為可以將其改寫為
$$
\frac{1}{2}\frac{d}{dr}(q’)^2 + \frac{d}{dr}e^q = 0
$$
即
$$
\frac{d}{dr}q = \pm\sqrt{2(C_1-e^q)}
$$
考慮積分常數為正且壓強關於半徑的導數為負,因此
$$
\frac{e^{-q/2}dq}{e^{-q/2}\sqrt{C_1-e^q}} = -\sqrt{2}dr
$$
即
$$
\frac{d[\sqrt{C_1}e^{-q/2}]}{\sqrt{C_1e^{-q}-1}} = \sqrt{C_1/2}dr
$$
其解為
$$
\sinh^{-1}[\sqrt{C_1}e^{-q/2}] = \sqrt{C_1/2}r + C_2
$$
整理得
$$
q = \ln C_1 - 2\ln\left[\sinh(\sqrt{C_1/2}r+C_2)\right]
$$
兩個參數要根據測量結果給出。
後記
結果如圖
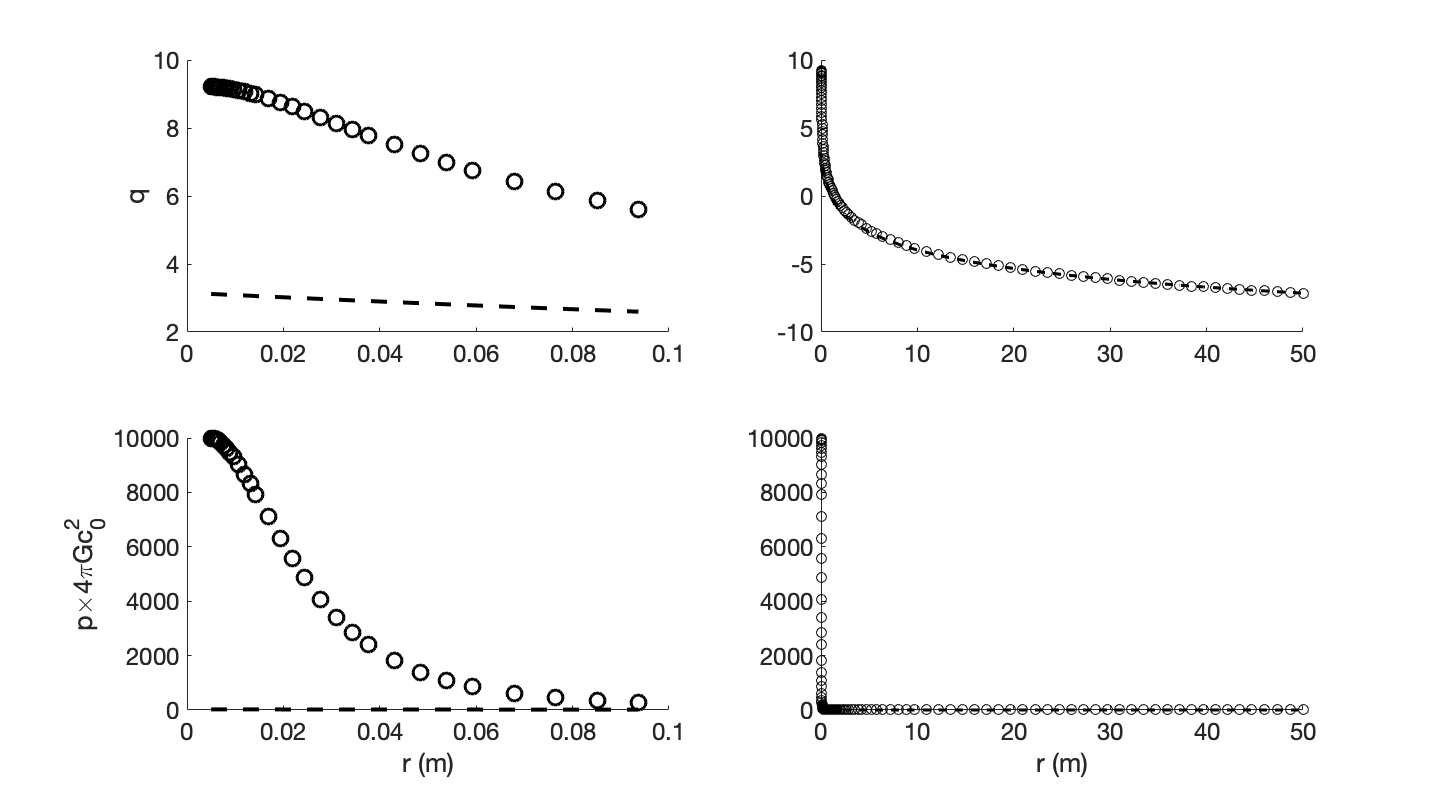
這裡圖示假設了初始位置$\tilde p$及其導數分別為10000及0.0001,圓點表示真實值而虛線表示近似值,可見近似效果在遠端是很好的。
雖然我不確定方程有沒有精確解,但它的變體是有的
$$
q’’ + \frac{1}{r}q’ + e^q = 0
$$
我傾向於認為沒有精確解。水平有限,我也不能證明這一點,儘管看上去非常簡單。
補充
考慮到遠端近似結果在近處偏差較大,換一種近似方法。
近端近似
注意到
$$
q’’ = \frac{\tilde p\tilde p’’ - (\tilde p’)^2}{\tilde p^2}
$$
由於靠近中心位置壓強很大,故略去這一項,因此將方程近似為
$$
2q’ + re^q \approx 0
$$
最後的指數項不能略去,兩邊同時乘以指數
$$
-q’e^{-q} = r/2
$$
積分得到
$$
e^{-q} = r^2/4 + c
$$
即
$$
q = -\ln\left[r^2/4+c\right]
$$
結果如圖
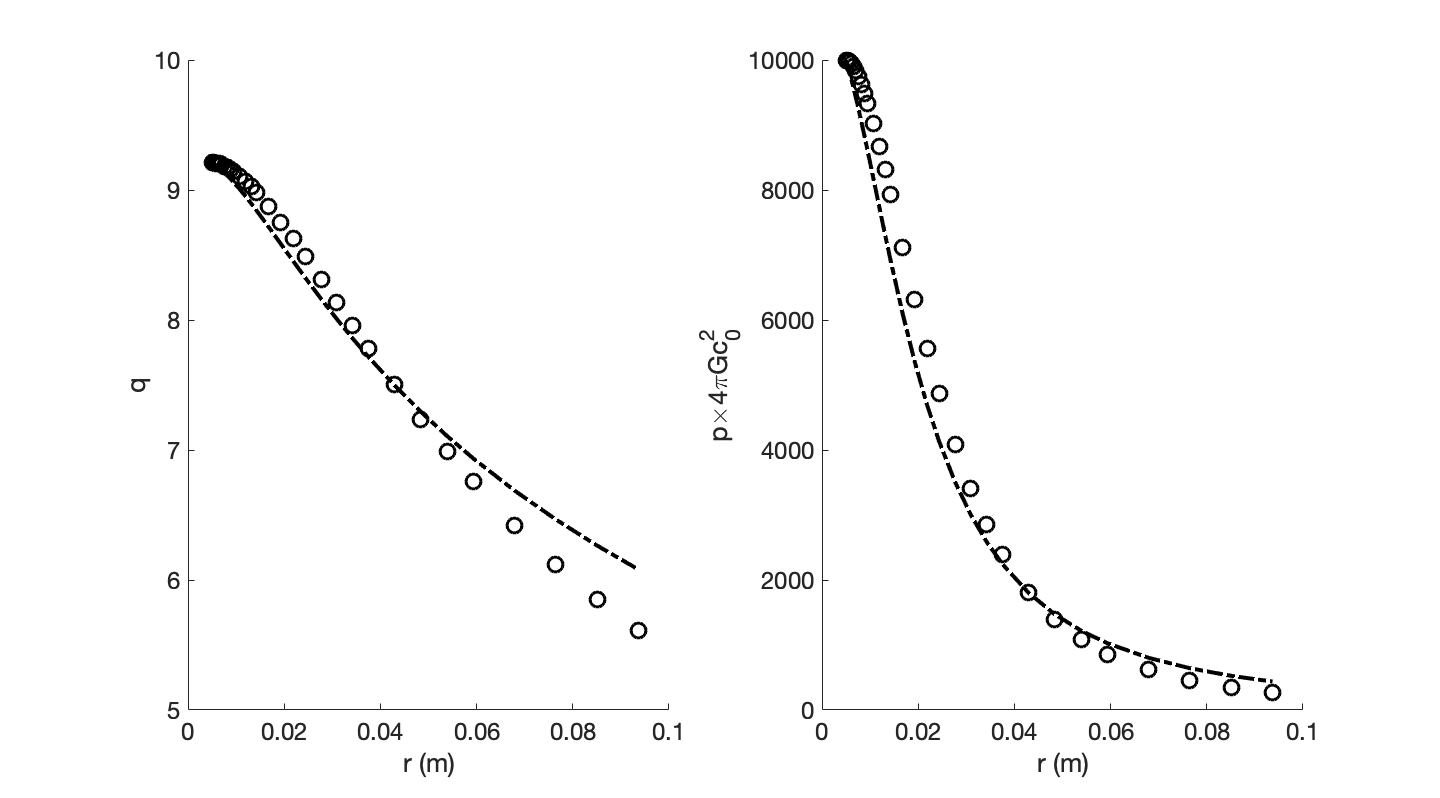
圓點表示真實值,點劃線為近似結果。