引言
早上我把門打開,和往常一樣,但我回房間的時候,發現門卻關不上了。
我這才留意到門板中部的變形,實際上在此之前我就曾聽到過摩擦產生的噪音,但沒有在意。我回想應該是多月來就沒有關過抽濕機的緣故,凹側對應一個低溼的環境,反過來,凸側對應的外部環境又因連日降雨,致使今天徹底關不上門。
雖然我不清楚木材的吸水膨脹性質,我也沒有學過,但我看到有個叫濕脹係數的東西,寫起來和楊氏模量這些我比較熟悉的材料屬性如出一轍。我假設它和我理解的性質是一樣的,並藉此計算形變的大小以及對應的曲率半徑。
模型
考慮一個原始長度為$l$的門板,內部水蒸氣濃度為$c_0$,寬度為$d$。現在置於一個水蒸氣濃度分別為$c_1$和$c_2$的環境中,分別標記為內側與外側。膨脹後外側的長度為$l_2$,內側為$l_1$。同時濕線膨脹係數為$\beta$。
計算
這個問題是很簡單的,考慮靜置足夠長的時間,內部的濕度是線性變化的,只需要觀察首尾就可以了。外側的伸長量滿足
$$
\frac{l_2 - l}{l} = \beta(c_2-c_0)
$$
同理內側有
$$
\frac{l_1 - l}{l} = \beta(c_1-c_0)
$$
不難發現首尾是不等長的,如果按照水分下降的分佈將其切割為無數個薄片的話,那麼最後應該呈現一個梯形的狀態,而不是一個弧。
這是有原因的,但這個原因與材料本身沒有關係,源自其他限制條件。這個原因是門板包漆,正是這一外部張力的存在,使得門板在發生細微變形的同時,而表面積盡可能不要發生變化,這才是門變成一個弧形的根本原因。
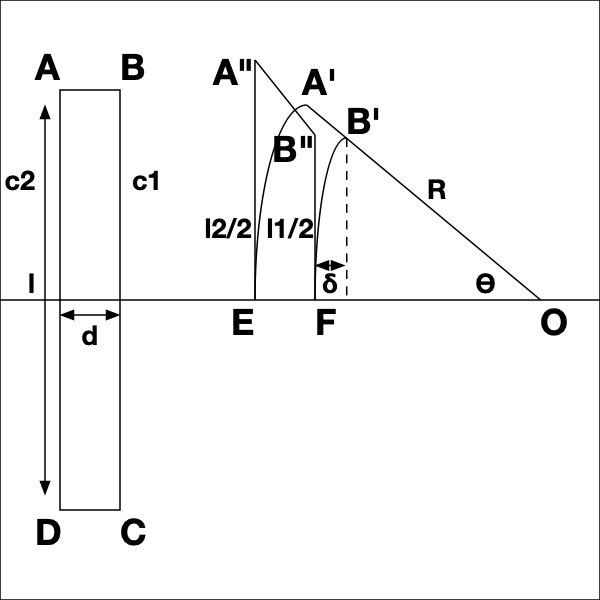
這是門板的一個剖面,取一半研究。注意變形後A、B點移至A”、B”處,設線段A”E與弧A’E、線段B”F與弧B’F的長度分別相等,即$l_1/2,l_2/2$。不難發現梯形A”B”FE與由兩段弧A’E、B’F構成的曲邊四邊形A’B’FE的面積是相等的,面積都等於$d(l_1+l_2)/4$。
但周長是不同的,梯形不含底邊EF的周長是:A”E+B”F+A”B”,而曲邊四邊形不含底邊EF的周長為:弧A’E+弧B’F+A’B’,前兩項完全相同,差別僅在最後一項。注意A’B’的長度等於EF,而EF為直角邊,顯然要小於斜邊A”B”。這樣也就證明了在保持相同面積的情況下,由兩段弧構成的曲邊四邊形可以顯著減小周長,換言之在三維情況下可以用較小的表面積實現一個較大的體積。
計算角度與曲率半徑
$$
(l_2-l_1)/2 = (R+d)\theta - R\theta = d\theta
$$
因此角度為
$$
\theta = \frac{l_2 - l_1}{2d} = \frac{l\beta(c_2-c_1)}{2d}
$$
曲率半徑為
$$
R = \frac{l_1}{2\theta} = \frac{1 + \beta(c_1-c_0)}{\beta(c_2-c_1)}d
$$
凸起量$\delta$為
$$
\delta = (R+d) - R\cos\theta - d = R(1-\cos\theta)
$$
當角度很小時,這一項就是零,將其展開
$$
\delta \approx R\frac{\theta^2}{2} = \frac{l_1\theta}{4} = \frac{l^2\beta(c_2-c_1)[1+\beta(c_1-c_0)]}{8d} \approx \frac{l^2\beta(c_2-c_1)}{8d}
$$
略去高階項,最後的結果正比於濃度差,雖然是很小的凸起,卻足以阻塞同樣狹窄的轉軸空隙,這也是我關不上門的原因。
後記
我也沒什麼辦法,看樣子只能等雨停。這也是我寫這篇文章的原因,閒著也是閒著。我往縫隙裡塗了點油,算是多少解決這個問題。
後來雨小了一點,我意外地發現門居然關上了,這真是一件令人欣慰的事情,雖然我基本上什麼也沒做。
頗具諷刺意味的是我雖然慫恿別人學物理,但我也很難解釋物理與普通人的日常生活有什麼關係。我能設想這樣一個情境,這是我少年時代觀看福爾摩斯探案集留下的印象。福爾摩斯與華生坐在車廂當中,突然,福爾摩斯告訴華生,當前火車前進的速度。
華生顯然很吃驚,一問才知道福爾摩斯一直在盯著手中的懷錶,並同時數著車廂外每隔幾米就架設的電線桿,聽上去沒有任何神奇之處。但我可能就未必會這麼做,我留意到車窗上常見的雨痕,在我看來你只需要測量一下雨痕的寬度與角度,就可以知道行進的速度。
當然講起來也沒有任何神奇之處,根據斯托克斯定律,雨滴下落存在重力與阻力的平衡
$$
6\pi\eta vr = \rho \frac{4\pi}{3}r^3g
$$
也就是說雨滴最終的下落速度與半徑平方成正比
$$
v = \frac{2\rho g}{9\eta}r^2
$$
雨滴相對車廂的速度,是雨滴相對地面的速度,加上地面相對車廂的速度,而後者與火車前進的速度$v_0$大小相同而方向相反。如果假設雨痕的寬度$d = 2r$,相對垂直方向的角度為$\phi$,那麼由簡單的幾何關係可以得到
$$
v_0 = v\tan\phi = \frac{\rho g}{18\eta}d^2\tan\phi
$$
這就是最後結果,或者反過來根據速度,特別是現在車廂一般附有速度讀數,求空氣的黏性係數$\eta$也是可以的。
但這些有什麼用呢,或許在有一天我被綁架的時候用得上。又或者就像今天一樣,用來打發無聊的旅途時間而已。