引言
幾天前,我留意到水中氣泡在底部留下一個明亮的光點,這讓我十分驚奇。空氣是光疏介質,無論如何也不會產生聚光效果。我想,可能氣泡的影子並不亮,只是在週遭的暗圈反襯下顯得格外明顯,這是我的一個猜想。
模型
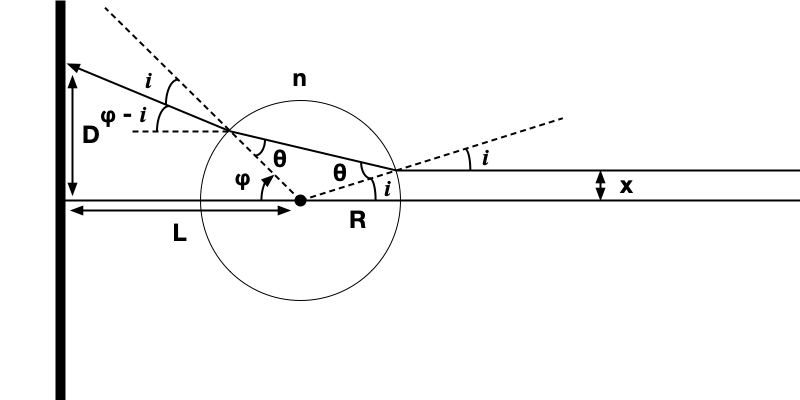
考慮一個水面下球形氣泡,半徑為$R$,球心到底部的距離為$L$。一束距離光軸為$x$的平行光射在氣泡表面,入射角為$i$,折射角為$\theta$。這束光照在底部距離光軸為$D$的位置,現在要找到$D$與$x$之間的函數關係。水的折射率$n = 1.33$,空氣的折射率近似為1,輔助角$\varphi$為出射點法線與光軸的夾角。
折射與反射
當光線距離光軸的距離超過半徑時,這種情況對應簡單的正投影。但在氣泡範圍內存在全反射的區間,因此要分三種情況討論。
折射
考慮近軸光線,假設全部光線均能進入氣泡中並被二次折射入液體內部。根據折射定律
$$
n\sin i = \sin\theta
$$
當$i = \arcsin(1/n)$時發生全反射,這裡考慮入射角要小於這個值。對入射角有
$$
\sin i = \frac{x}{R}
$$
這樣所有的角均可解出,同時輔助角$\varphi = 2\theta -i$。由簡單的三角關係可以得到
$$
\frac{D - R\sin\varphi}{L - R\cos\varphi} = \tan(\varphi -i)
$$
全反射
這種情況光線遠離光軸,但還在氣泡範圍內。由於入射角大於臨界角,所有光線被嚴格反射,根據三角關係有
$$
\frac{D - R\sin(\pi -i)}{L - R\cos(\pi -i)} = \tan(\pi -2i)
$$
正投影
這種情況最為簡單$D = x$。
光線密度
由上述結論可以寫出$D$關於$x$的函數。根據折射定律$n\sin i = \sin\theta$,折射角$\sin i = \frac{x}{R}$以及輔助角$\varphi = 2\theta - i$可以得到隱式結果。當$0 \leq x \leq R/n$時
$$
D_1 = R\sin\varphi + (L-R\cos\varphi)\tan(\varphi -i)
$$
當$R/n < x \leq R$時
$$
D_2 = x - (L+R\cos i)\tan(2i)
$$
當$x > R$時
$$
D_3 = x
$$
分別計算關於$x$的導數,這在接下來的討論中會用到。對$D_1(x)$
$$
D_1’(x) = R\varphi’(x)\cos\varphi + R\varphi’(x)\sin\varphi\tan(\varphi -i) + (L-R\cos\varphi)[\varphi’(x)-i’(x)]\sec^2(\varphi -i)
$$
對$D_2(x)$
$$
D_2’(x) = 1 + xi’(x)\tan(2i) - 2(L+R\cos i)\sec^2(2i)
$$
以及$D_3’(x) = 1$,其中$\varphi’(x) = 2\theta’(x) - i’(x)$,$i’(x) = \frac{1}{\sqrt{R^2 - x^2}}$,$\theta’(x) = \frac{n}{\sqrt{R^2 - n^2x^2}}$。
密度
這裡把問題簡化為一維。假設平行光均勻分佈,其在$x$方向的光線密度為$\rho_0$。如果$D$(x)是一個單調增加函數,考慮守恆關係
$$
\rho dD = \rho_0dx
$$
其中$dD$為$D$方向上的小段距離。這樣不難得到
$$
\rho = \rho_0 \frac{1}{\frac{dD}{dx}} \propto \frac{1}{D’(x)}
$$
但這裡要做幾點說明。
首先$D(x)$是一個單調函數即可,表達式中應該替換為絕對值。其次上述公式中密度$\rho$是$x$的函數,而非$D$,即可以用上述公式計算對密度的貢獻,但要把最後結果中的$x$換成$D$。$D(x)$的反函數$x(D)$要複雜得多,直接計算導數幾乎不可能,而且還是一個多值函數。因此需要根據一個給定的$D$,尋找對應的$x$,利用上述公式考慮每一段單調函數的貢獻。即
$$
\rho \propto \frac{1}{|D_1’(x)|} + \frac{1}{|D_2’(x)|} + \frac{1}{|D_3’(x)|}
$$
而公式中出現的$x$應分別替換為$x_1(D)$,$x_2(D)$與$x_3(D)$。
結果
中心亮度可以計算為
$$
\rho(D=0) = \frac{1}{2n - 1 + 2(n-1)(\frac{L}{R}-1)}
$$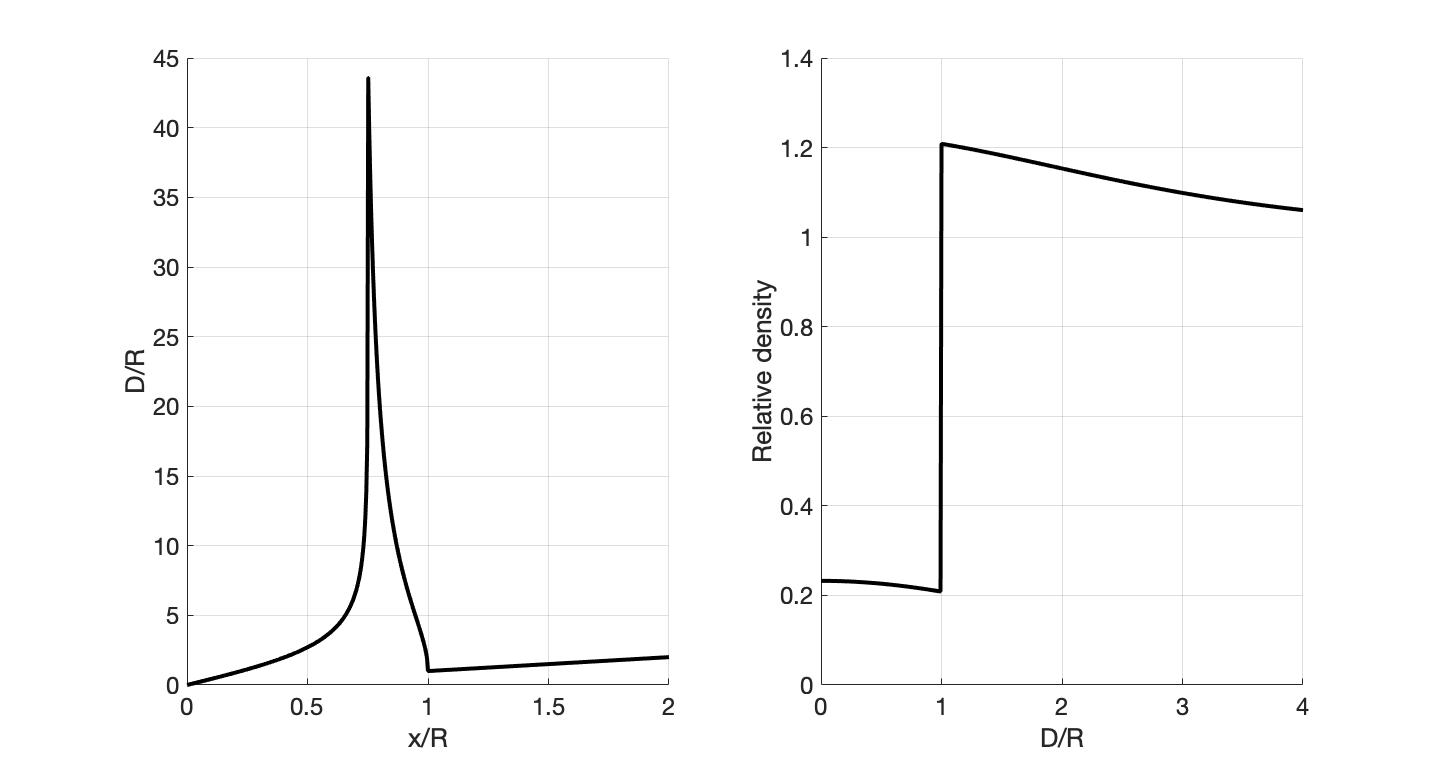
由於涉及到反函數求解,因此結果只能通過數值方法計算。左邊的尖峰對應臨界角附近的全反射情況,而右邊則告訴你氣泡影子的中心點雖然比週遭亮一些,但還沒亮到能讓你察覺的程度。事實上,氣泡留下一塊與自身大小相同的暗影,而週遭環繞一圈亮邊:這個亮邊不只相對暗影來說,更相對背景都亮一點,這當然是折射導致的疊加效果。
後記
這個問題可以複雜也可以簡單。譬如說,光線在氣泡內部會發生多次折射與反射,你實質上得到一個級數和,而且其形式不會簡單。更何況,幾何光學不能處理透射率的問題,這屬於電動力學在邊界處理上的應用。事實上就是最後的光強,我也不知道如何計算。但如果我把這些都考慮在內,這個問題就變得極為複雜了。
在近軸情況下反射率極小,可以近似認為所有光線都進入了氣泡,而且忽略多次折射與反射。此外,我只考慮大於臨界角的反射,當然是不準確的,因為這是一個連續的過程。臨界角約為四十九度,而入射角需要超過四十五度才對背景有貢獻,可以近似認為它們是相同的。此外考慮到臨界角附近的光線會經過兩次折射或一次反射到很遠的地方,恰如結果所示的尖峰,而我在計算光線密度所用到的$D$根本不會考慮到那麼遠的地方,所以這個近似也是沒問題的。最後光強問題,我將其近似處理為無數條微小光束的密度,這樣的微小光束的數目在$x$與$D$處的統計,當然是守恆的。關於這一點,我從沒見到別人用類似的方式處理過。
我確實觀察到理論預測的暗影現象,證明計算結果是正確的。然而我又觀察到那個我無法解釋的亮斑,事實上前者因為較暗反而不易被察覺。這實在令人失望,我實在想不到有什麼辦法能夠解釋它。如果我起初觀察到的是暗影現象,我是不會寫這篇文章,因為那不過是意料之中的事情。