引言
用年齡密度描述人群中數量分佈,求解其對應的動力學方程。
物理模型
考慮年齡密度$\rho(x,t)$是年齡$x(x>0)$與時間$t(t>0)$的二元函數。已知初始密度分佈$\rho(x,0)$,以及各個年齡層的死亡率分佈$D(x)$與生育概率分佈$B(x)$。平均生育人數為$n$,其意義由後續討論可知,同時用$v$表示年齡分佈隨時間整體平移速率。
考慮年齡層$x$在$t+dt$時刻的分佈人數$\rho(x,t+dt)dx$,主要其來自$t$時刻年齡層$x-dx$的貢獻,並扣除對應的死亡人數。
$$
\rho(x,t+dt)dx = \rho(x-dx,t)dx - D(x-dx)\rho(x-dx,t)dx^2
$$
整理可以得到
$$
\begin{aligned}
\rho(x,t+dt) - \rho(x,t) + \rho(x,t) - \rho(x-dx,t) =& -D(x-dx)\rho(x-dx,t)dx\nonumber\\
\frac{\partial\rho(x,t)}{\partial t}dt + \frac{\partial\rho(x,t)}{\partial x}dx \approx& -D(x)\rho(x,t)dx
\end{aligned}
$$
兩邊同時除以$dt$,並考慮到$dx = vdt$,得到人口模型對應動力學方程
$$
\frac{\partial\rho(x,t)}{\partial t} + v\frac{\partial\rho(x,t)}{\partial x} + vD(x)\rho(x,t) = 0
$$
結合初始條件$\rho(x,0)$即可求解。但此類問題還有一個邊界條件,即$t$時刻出生人數與此時刻的密度分佈有關,直接寫出邊界條件
$$
\rho(0,t) = \int_0^\infty nB(x)\rho(x,t)dx
$$
人口方程
已知人口動力學方程
$$
\frac{\partial\rho(x,t)}{\partial t} + v\frac{\partial\rho(x,t)}{\partial x} + vD(x)\rho(x,t) = 0
$$
與初始密度分佈$\rho(x,0)$及邊界條件
$$
\rho(0,t) = \int_0^\infty nB(x)\rho(x,t)dx
$$
其中$D(x)$與$B(x)$由實際觀測數據測量得到。
注意到這是一個一階線性偏微分方程,可以用特徵線法解出。特徵線方程
$$
dt = \frac{dx}{v} = -\frac{d\rho}{vD\rho}
$$
解出$x = x_0 + vt$與$\rho = \rho_0e^{-\int_0^x D(\tau)d\tau}$。
但注意到初始密度分佈與邊界條件兩者只需其一,因此需要分成兩部分討論。
當x>vt時
這種情況較為簡單,即最先出生的人口還不足以影響到$x$年齡層,此時影響到該年齡密度的主要來自初始密度分佈$\rho(x,0)$。考慮$t=0$時,有$x = x_0$,$\rho = \rho_0e^{-\int_0^{x_0}D(\tau)d\tau}$,代入初始密度
$$
\rho(x_0,0) = \rho_0e^{-\int_0^{x_0}D(\tau)d\tau}
$$
利用$x_0 = x - vt$與$\rho_0 = \rho e^{\int_0^xD(\tau)d\tau}$消去$x_0$與$\rho_0$,得到
$$
\rho(x,t) = \rho(x-vt,0)e^{-\int_{x-vt}^xD(\tau)d\tau}
$$
結果為顯式解。
當x<vt時
這種情況較為複雜,影響到$x$年齡層的不再來自初始密度分佈,而是來自初始時刻之後出生的人口。需要用到邊界條件$\rho(0,t) = \int_0^\infty B(x)\rho(x,t)dx$。考慮$x = 0$時,有$x_0 = -vt$,$\rho = \rho_0$,代入邊界條件
$$
\rho(0,-\frac{x_0}{v}) = \rho_0
$$
利用$x_0 = x - vt$與$\rho_0 = \rho e^{\int_0^xD(\tau)d\tau}$消去$x_0$與$\rho_0$,得到
$$
\rho(x,t) = \int_0^\infty nB(\tau)\rho(\tau,t-\frac{x}{v})d\tau e^{-\int_0^xD(\tau)d\tau}
$$
結果為隱式解,需要知道密度分佈在此前$t - \frac{x}{v}$時刻的分佈。
討論
已知人口方程的解為
$$
\rho(x,t) = \rho(x-vt,0)e^{-\int_{x-vt}^xD(\tau)d\tau}
$$
對應$x - vt > 0$位置,此外有
$$
\rho(x,t) = \int_0^\infty nB(\tau)\rho(\tau,t-\frac{x}{v})d\tau e^{-\int_0^xD(\tau)d\tau}
$$
對應$x - vt < 0$位置。$D(x)$與$B(x)$根據實際情況修正,注意到兩者均可為時間的函數,但在一個處於穩態的社會裡,可以認為僅與年齡有關。
死亡
死亡率分佈$D(x)$大致為一個倒三角曲線,除去在初始時刻有一個不連續的峰:這對應於嬰兒的高夭折率。處理時應將其分離出來,在平均生育人數$n$中扣除。為方便計算,假設人口壽命閾值為$x_m$,其意義由後續討論給出,$D(x)$在$(0,x_m)$上做歸一化處理並要求發散,假設滿足
$$
D(x) = \frac{k}{x_m(e^k-1)}e^{\frac{k}{x_m}x}
$$
$k$為待定參數。這樣第一個解可以簡化為
$$
\rho(x,t) = \rho(x-vt,0)\exp[-\frac{e^{\frac{k}{x_m}x}}{e^k - 1}(1-e^{-\frac{kvt}{x_m}})]
$$
生育
$B(x)$為已扣除夭折的生育概率分佈,假設嬰兒死亡率與幼兒死亡率相當,除去中部可能出現雙峰外,則大致為一個鍾形曲線,假設其服從高斯分佈
$$
B(x) = \frac{\exp[-\frac{(x-\mu)^2}{2\sigma^2}]}{\sigma\sqrt{2\pi}}
$$
$\mu$為平均生育年齡,$\sigma$為標準差。考慮一個極端情況,當方差趨近零,將得到Delta函數$\delta(x-\mu)$。即積分將直接得到$n\rho(\mu,t-\frac{x}{v})$,對應平均生育年齡。這種近似與實際的區別在於考慮死亡對生育人數的影響,而這種差異可以被其他參數平均掉。在這種情況下第二個解可以被進一步簡化
$$
\rho(x,t) = n\rho(\mu,t-\frac{x}{v})\exp[-\frac{e^{\frac{k}{x_m}x} - 1}{e^k - 1}]
$$
穩定
上述簡化使得分析穩定人口狀態成為可能,考慮穩定狀態下有$\rho(\mu,t) = \rho(\mu,t-\frac{x}{v}) = \rho_c$,得到穩恆狀態下人口密度分佈
$$
\rho(x) = n\rho_c\exp[-\frac{e^{\frac{k}{x_m}x} - 1}{e^k - 1}]
$$
注意到這裡的閾值$x_m$不是壽命上限,其含義為穩定社會出生存活人口下降到$1/e$時對應的截斷年齡。可以計算穩定狀態下的總人口$N$為
$$
N = \int_0^\infty\rho(x)dx = \frac{n\rho_cx_m\exp[\frac{1}{e^k - 1}]}{k}[-\text{Ei}(-\frac{1}{e^k - 1})]
$$
其中$\text{Ei}(z)$為指數積分函數,同時得到穩定狀態平均生育年齡$\mu_c$為
$$
\mu_c = \frac{x_m}{k}\ln[(e^k-1)\ln n+1]
$$
當$\mu < \mu_c$時,有$\rho(\mu,t) > \rho(\mu,t-\frac{x}{v})$,意味著人口將膨脹。由於$k$是死亡分佈的量度,越大意味著青壯年死亡率越低,反之對應貧窮社會。考慮一個極端情況,當$k$趨近於零時,有非常簡單的關係
$$
\frac{\mu_c}{x_m} = \ln n
$$
事實上這樣極度貧窮卻又穩定的社會並不多見。以非洲為例,計算出的$\mu_c$實質上遠大於平均婚育年齡,意味著該地區人口在急遽膨脹。
當$\mu > \mu_c$時,有$\rho(\mu,t) < \rho(\mu,t-\frac{x}{v})$,意味著人口將萎縮。一個例子是富裕地區平均婚育人數$n$通常小於一,即$\mu_c$為負數,可知對應人口的萎縮。
實際上這樣的平衡是脆弱的。另一個有意思的角度是:當貧窮社會$(\mu < \mu_c)$採用推遲婚育年齡(增大$\mu$),節制生育(降低$\mu_c$)等手段達成平衡以期望控制人口,前者或可奏效,而後者是愚蠢的,列寧國家或可嘗試強制生育和計畫死亡。
模式
解出穩恆狀態下人口密度分佈
$$
\rho(x) = n\rho_c\exp[-\frac{e^{\frac{k}{x_m}x} - 1}{e^k - 1}]
$$
分佈曲線與實際情況是吻合的,說明討論中的簡化假設為合理近似。下面對不同$k$與$x_m$值劃分出兩種社會模式
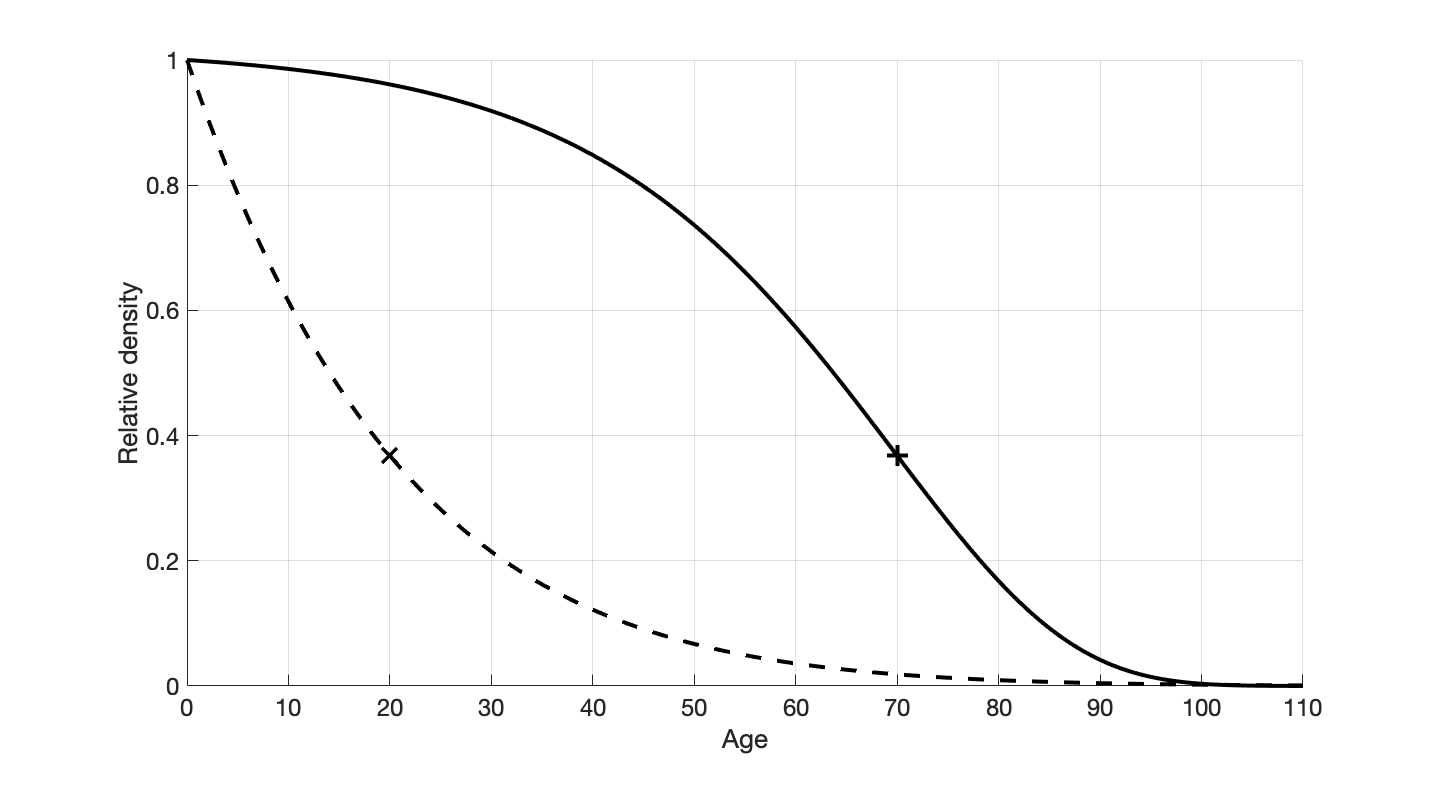
富裕社會
高$k$值與高$x_m$值,形似蘿蔔,這對應人口演化的一個穩定解。圖中實線,符號對應截斷年齡七十歲,$k$值取4。
貧困社會
低$k$值與低$x_m$值,形似尖銳的金字塔,這同樣對應人口演化的一個穩定解。圖中虛線,符號對應截斷年齡二十歲,$k$值取0.1。
後記
這篇文章靈感來源於幾日前我注意到大陸畸形的人口結構,那些像盤子一樣堆疊起來的人口金字塔圖,讓我想到流體力學模型:這或許是一個簡單的問題⋯
我在組會上隨手推導了人口的動力學方程,雖然我一開始並不清楚各個參數的意義。這麼多年我已經習慣於方程無法直接求解,用數值方法把圖像畫一下。但我覺得這樣一點意思都沒有,考慮幾個近似條件,得到解析解的形式。
雖然我的初衷是計算大陸人口變化,但那心電圖似的人口密度曲線,讓我實在懶得做這事。文中只對穩定情況做了討論,事實上穩定情況是不多見的。相信現實會有細微的偏離,對應略微偏離穩態的情況,故形狀應該類似,結果大差不差。
一個經驗是好的模型是常常是簡潔的:把複雜度扔給參數,而不是讓模型本身的物理圖像變得複雜。